Reduction formula
A properly chosen set of functions or coordinates can be used as a basis for a representation. Usually, the representation
( ) can be splitted into irreducible representations (
) can be splitted into irreducible representations ( irrep). Examples for common basis sets in chemistry are:
irrep). Examples for common basis sets in chemistry are:
- The set of 3N (N: number of atoms) cartesian coordinates (
 3N).
3N).
- The set of molecular vibrations (
 vib).
vib).
- The atomic basis functions in a LCAO-MO calculation (
 AO).
AO).
- A special case of a
 AO-representation is the representation for the valence orbitals (
AO-representation is the representation for the valence orbitals ( valence).
valence).
- The
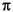 -orbitals in the Hückel approximation (
-orbitals in the Hückel approximation (
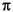 ).
).
Details about the construction of representations can be found in books about group theory.
This WWW project allows the reduction of reducible representations to irreducible representations. As an example the 
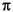 -representation for the
-representation for the 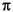 -orbitals in benzene (point group D6h) is given.
-orbitals in benzene (point group D6h) is given.
| E |
2C6 (z) |
2C3 |
C2 |
3C'2 |
2C''2 |
i |
2S3 |
2S6 |
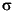 h (xy) h (xy) |
3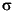 d d |
3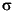 v v |
| 6 |
0 |
0 |
0 |
-2 |
0 |
0 |
0 |
0 |
-6 |
0 |
2 |
This representation can be reduced to:

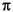 =
=  b2g +
b2g +
 e1g +
e1g +
 a2u +
a2u +
 e2u
e2u
In case of a molecular 3N representation ( 3N) the contributions for translational and
rotational modes are removed automatically. The resulting vibrational representation (
3N) the contributions for translational and
rotational modes are removed automatically. The resulting vibrational representation ( vib)
is used to determine the symmetry properties of the force constants up to the quartic force field. As an example the molecular 3N
representation for chloroform (point group C3v) is given.
vib)
is used to determine the symmetry properties of the force constants up to the quartic force field. As an example the molecular 3N
representation for chloroform (point group C3v) is given.
| E |
2C3 (z) |
3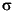 v v |
| 15 |
0 |
3 |
This representation can be reduced to:
 3N = 4
3N = 4 a1 +
a1 +
 a2 +
5
a2 +
5 e
e
The corresponding vibrational representation can be reduced to:
 3N = 3
3N = 3 a1 +
3
a1 +
3 e
e
Since the number of independant internal coordinates is equal to the number of totally symmetrical vibrations
it can be seen easily that chloroform possesses in C3v symmetry only 3 degrees of freedom. The force
field analysis shows that there are only up to 12 nonvanishing unique quadratic force constants. The
analogous procedure for the cubic (quartic) force field shows that there are only 38 (102) nonvanishing
unique cubic (quartic) force constants.



Last update Mai, 23rd 2018 by A. Gelessus, Impressum, Datenschutzerklärung/DataPrivacyStatement
 3N).
3N).
 vib).
vib).
 AO).
AO).
 AO-representation is the representation for the valence orbitals (
AO-representation is the representation for the valence orbitals ( valence).
valence).
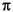 -orbitals in the Hückel approximation (
-orbitals in the Hückel approximation (
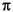 ).
).
 ) can be splitted into irreducible representations (
) can be splitted into irreducible representations ( irrep). Examples for common basis sets in chemistry are:
irrep). Examples for common basis sets in chemistry are:
 3N).
3N).
 vib).
vib).
 AO).
AO).
 AO-representation is the representation for the valence orbitals (
AO-representation is the representation for the valence orbitals ( valence).
valence).
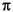 -orbitals in the Hückel approximation (
-orbitals in the Hückel approximation (
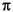 ).
).

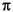 -representation for the
-representation for the 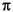 -orbitals in benzene (point group D6h) is given.
-orbitals in benzene (point group D6h) is given.
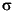 h (xy)
h (xy)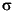 d
d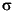 v
v
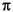 =
=  b2g +
b2g +
 e1g +
e1g +
 a2u +
a2u +
 e2u
e2u
 3N) the contributions for translational and
rotational modes are removed automatically. The resulting vibrational representation (
3N) the contributions for translational and
rotational modes are removed automatically. The resulting vibrational representation ( vib)
is used to determine the symmetry properties of the force constants up to the quartic force field. As an example the molecular 3N
representation for chloroform (point group C3v) is given.
vib)
is used to determine the symmetry properties of the force constants up to the quartic force field. As an example the molecular 3N
representation for chloroform (point group C3v) is given.
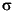 v
v 3N = 4
3N = 4 a1 +
a1 +
 a2 +
5
a2 +
5 e
e
 3N = 3
3N = 3 a1 +
3
a1 +
3 e
e


