Reduction formula for point group I
Your representation
| E |
12C5 |
12(C5)2 |
20C3 |
15C2 |
| 180 |
0.0000 |
-0.0000 |
0 |
0 |
can be reduced to
Substraction of translational and rotational contributions results in
Force field analysis
Infrared and Raman activities (harmonic approximation)
| Method |
A |
T1 |
T2 |
G |
H |
| Infrared |
- |
+ |
- |
- |
- |
| Raman |
+ |
- |
- |
- |
+ |
Number of force field parameters
| Force field |
No. 1 |
No. 2 |
No. 3 |
| linear |
174 |
174 |
3 |
| quadratic |
30276 |
15225 |
277 |
| cubic |
5268024 |
893200 |
14948 |
| quartic |
916636176 |
39524100 |
659737 |
No. 1 : Total number of force constants 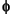 .
.
No. 2 : Total number of force constants k.
No. 3 : Total number of nonvanishing force constants k.
Symmetry properties of force field parameters
| Force field |
A |
T1 |
T2 |
G |
H |
| linear |
3 |
7 |
9 |
12 |
15 |
| quadratic |
277 |
741 |
738 |
1014 |
1291 |
| cubic |
14948 |
44614 |
44616 |
59568 |
74458 |
| quartic |
659737 |
1975206 |
1975203 |
2634939 |
3294676 |
| Number of independant internal coordinates |
3 |
Literature
- J.K.G. Watson, J. Mol. Spec. 41 229 (1972)
The Numbers of Structural Parameters and Potential Constants of Molecules



Last update November, 13th 2023 by A. Gelessus, Impressum, Datenschutzerklärung/DataPrivacyStatement
 .
.

