Force field analysis for point group D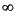 h
h
Number of atoms: 4
Your  3N representation
3N representation
| E |
2C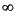 |
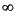  v v |
i |
2S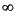 |
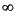 C'2 C'2 |
| 12 |
4+ 8cos(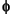 ) ) |
4 | 0 |
0 |
0 |
can be reduced to
A1g= +g +g |
A2g= -g -g |
E1g= g g |
E2g= g g |
E3g= g g |
E4g= g g |
A1u= +u +u |
A2u= -u -u |
E1u= u u |
E2u= u u |
E3u= u u |
E4u= u u |
| 2 |
0 |
2 |
0 |
0 |
0 |
2 |
0 |
2 |
0 |
0 |
0 |
Substraction of translational and rotational contributions results in
A1g= +g +g |
A2g= -g -g |
E1g= g g |
E2g= g g |
E3g= g g |
E4g= g g |
A1u= +u +u |
A2u= -u -u |
E1u= u u |
E2u= u u |
E3u= u u |
E4u= u u |
| 2 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
Infrared and Raman activities (harmonic approximation)
| Method |
A1g= +g +g |
A2g= -g -g |
E1g= g g |
E2g= g g |
E3g= g g |
E4g= g g |
A1u= +u +u |
A2u= -u -u |
E1u= u u |
E2u= u u |
E3u= u u |
E4u= u u |
| Infrared |
- |
- |
- |
- |
- |
- |
+ |
- |
+ |
- |
- |
- |
| Raman |
+ |
- |
+ |
+ |
- |
- |
- |
- |
- |
- |
- |
- |
No. 1 : Total number of force constants 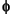 .
.
No. 2 : Total number of force constants k.
No. 3 : Total number of nonvanishing force constants k.
Symmetry properties of force field parameters
| Force field |
A1g= +g +g |
A2g= -g -g |
E1g= g g |
E2g= g g |
E3g= g g |
E4g= g g |
A1u= +u +u |
A2u= -u -u |
E1u= u u |
E2u= u u |
E3u= u u |
E4u= u u |
| linear |
2 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
| quadratic |
6 |
0 |
3 |
2 |
0 |
0 |
3 |
1 |
3 |
1 |
0 |
0 |
| cubic |
11 |
1 |
9 |
5 |
2 |
0 |
8 |
2 |
9 |
4 |
2 |
0 |
| quartic |
23 |
3 |
19 |
14 |
6 |
3 |
16 |
6 |
19 |
12 |
6 |
2 |
| Number of independant internal coordinates |
2 |
Literature
- J.K.G. Watson, J. Mol. Spec. 41 229 (1972)
The Numbers of Structural Parameters and Potential Constants of Molecules



Last update November, 21th 2023 by A. Gelessus, Impressum, Datenschutzerklärung/DataPrivacyStatement
 h
h 3N representation
3N representation
 v
v )
) +g
+g -g
-g g
g g
g g
g g
g +u
+u -u
-u u
u u
u u
u u
u +g
+g -g
-g g
g g
g g
g g
g +u
+u -u
-u u
u u
u u
u u
u +g
+g -g
-g g
g g
g g
g g
g +u
+u -u
-u u
u u
u u
u u
u .
. +g
+g -g
-g g
g g
g g
g g
g +u
+u -u
-u u
u u
u u
u u
u

